Можно ли в регрессии использовать неколичественные переменные?
Можно ли в регрессии использовать неколичественные переменные?
Однозначно можно сказать, что они не могут быть использованы в качестве зависимой переменной Y. Это будет грубейшей ошибкой; в этом случае уравнением регрессии может быть предсказан, к примеру, пол имеющий код 1.5 или 0.5 при общепринятой кодировке пола 1-мужчины, 2-женщины. Может быть, это как-то интерпретируется с медицинской точки зрения, но в практике социальных исследований это будет едва ли возможно.
Для использования в качестве независимой переменной применяются индексные переменные (в англоязычной литературе dummy-variables).
Например, для семейного положения в данных Курильского обследования (женат, вдов, разведен, холост) стоит ввести три индикаторные переменные t1, t2 и t3 для выделения женатых, вдовых, и разведенных. Эти переменные будут равны, соответственно единице или нулю, в зависимости от того принадлежит или не принадлежит респондент к соответствующей группе по семейному положению.
Почему не 4 индексные переменные? Четвертая переменная определяется однозначно через первые три, поэтому, введение ее вызвало бы коллинеарность, не позволяющую найти коэффициенты регрессии.
Вот задание, которое позволяет изучить зависимость душевого дохода от возраста и семейного положения:
compute lnv14m =ln(v14/200).
compute t1=(v11=1).
compute t2=(v11=2).
compute t3=(v11=3).
Compute v9_2=v9**2.
*квадрат возраста.
REGRESSION /DEPENDENT lnv14m /METHOD=ENTER v9 v9_2 t1 t2 t3 /SAVE PRED.
График связи возраста (V9) с предсказанным уравнением логарифмом доходов (переменная pre_2) получается командой
GRAPH /SCATTERPLOT(BIVAR)=v9 WITH pre_2 /MISSING=LISTWISE
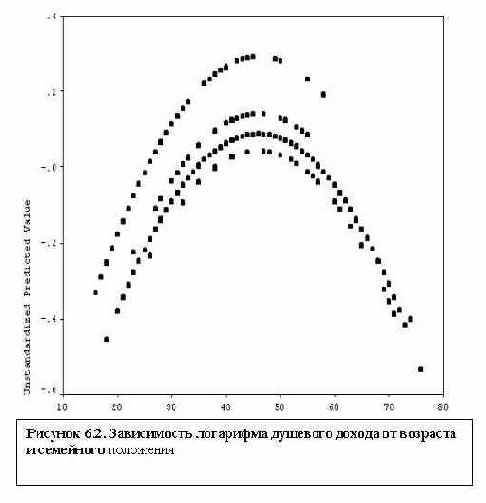
Он представляет собой 4 параболы (рисунок 6.2). В соответствии с коэффициентами перед t1, t2 и t3 (см. таблицу 6.4), эти пораболы соответствуют, сверху вниз, холостякам, разведенным, женатым и вдовцам (порабола холостяков получается при t1=t2=t3=0).
Вероятно, полученное уравнение можно улучшить, исключив из уравнения переменные с незначимыми коэффициентами. Поскольку индексные переменные должны быть в определенной степени взаимосвязаны, уровень наблюдаемой значимости может определяться здесь коллинеарностью, поэтому "ревизию" переменных нужно проводить осторожно, чтобы существенно не ухудшить полученного уравнения.
Из-за взаимосвязи переменных здесь нет возможности говорить о том, какая переменная больше влияет на зависимую переменную. Обратите внимание на довольно редкий эффект: бета-коэффициенты для возраста и его квадрата по абсолютной величине больше 1!