Коэффициенты регрессии.
Таблица 6.3. Коэффициенты регрессии.
|
Unstandardized Coefficients |
Standardized Coefficients |
T |
Sig. | ||
|
B |
Std. Error |
Beta | |||
|
(Constant) |
-1.0569 |
0.1888 |
-5.5992 |
0.0000 | |
|
V9 Возраст |
0.0505 |
0.0093 |
1.1406 |
5.4267 |
0.0000 |
|
V9_2 |
-0.0006 |
0.0001 |
-1.0829 |
-5.1521 |
0.0000 |
Регрессионные коэффициенты представлены в таблице 6.3. В соответствии с ними, уравнение регрессии имеет вид
Лог.промед.дохода = -1.0569+0.0505*возраст-0.0006*возраст2
Стандартная ошибка коэффициентов регрессии значительно меньше величин самих коэффициентов, их отношения - t статистики, по абсолютной величине больше 5. Наблюдаемая значимость статистик (Sig) равна нулю, поэтому гипотеза о равенстве коэффициентов нулю отвергается для каждого коэффициента. Стоит обратить внимание на редкую ситуацию - коэффициенты бета по абсолютной величине больше единицы. Это произошло, по-видимому, из-за того, что корреляция между возрастом и его квадратом весьма велика.
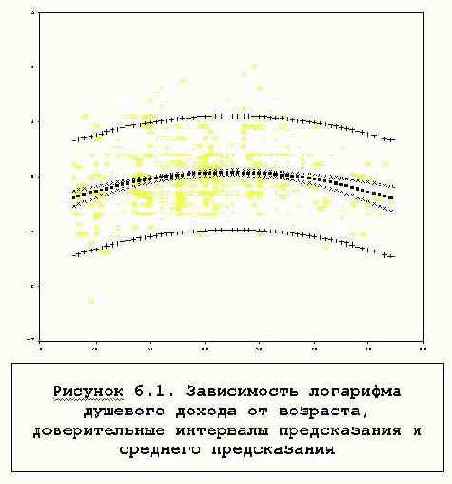
Рисунок 6.1 показывает линию регрессии и доверительные границы для M(y) - матожидания y и для индивидуальных значений y. Он получается с помощью наложения полей рассеяния возраста с зависимой переменной, с переменной - прогнозом, с переменными - доверительными границами:
GRAPH /SCATTERPLOT(OVERLAY)=v9 v9 v9 v9 v9 v9 WITH pre_1 lmci_1 umci_1 lici_1 uici_1 lnv14m(PAIR).
Границы для M(y) значительно уже, чем для y, так как последние должны охватывать больше 95% точек графика.
На графике не прослеживается явной зависимости дисперсии остатка от значений независимой переменной - возраста. Некоторое сужение рассеяния данных для старших возрастов произошло, вероятно, за счет общего уменьшения плотности двумерного распределения.