Тест Хи-квадрат

5.1.1. Тест Хи-квадрат

Критерий Хи-квадрат основан на статистике

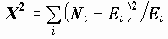
где

- ожидаемая частота i-го значения переменной, Ni расчетная. Теоретическое распределение этой статистики при больших N совпадает с распределением Хи-квадрат. Число степеней свободы теоретического распределения полагается равным k-1, где k - число значений исследуемой переменной. Эмпирическое правило говорит о том, что некорректно применять критерий, если ожидаемые частоты меньше 5, поскольку его распределение в этом случае не будет близко к теоретическому. Но использование точных методов вычисления значимости (метод Монте-Карло) позволяет избежать этого ограничения.

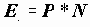
Пример. Пусть, согласно статистическим данным, 30% трудоспособного населения имеют возраст до 30 лет, 30% - от 30 до 40 лет и 40% свыше 40 лет. Соответствует ли выборочное распределение признака "возраст" в обследовании "Курильские острова" распределению возраста в генеральной совокупности?

RECODE v9 (1 THR 30 =1)(31 THR 40 =2)(41 THRU HI =3) INTO w9.

NPAR TESTS /CHISQUARE = W9 /EXPECTED 3 3 4.

Подкоманда /CHISQUARE задает тестируемую переменную; в подкоманде /EXPECTED задаем через пробел ожидаемые пропорции распределения.

Выполнение этих команд позволяет получить значение критерия и оценить степень соответствия нашей выборки распределению генеральной совокупности (табл. 5.1, 5.2).

Содержание раздела