Моделирование и обработка статистических данных
При использовании в научных и инженерных исследованиях метода статистического моделирования (метод Монте-Карло) необходимо генерировать случайные (точнее, псевдослучайные) числа, распределенные по определенному закону.
Функции MathCAD для вычисления плотности распределения. В табл. 10.1.1 приведены функции (имена начинаются с буквы d), позволяющие вычислить значения функции плотности наиболее используемых распределений (

Таблица 10.1.1
| Распределение | Функция MathCAD | ||
Нормальное распределение
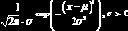 | 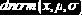 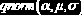 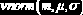 | ||
Распределение Пуассона
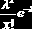 (   | 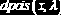 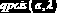 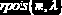 | ||
Равномерное распределение
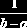 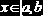 0, если 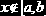 | 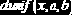 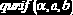 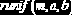 | ||
Биноминальное распределение
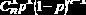 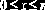 | 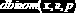 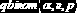 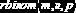 |
Окончание табл. 10.1.1
| Распределение | Функция MathCAD | ||
 0, если 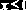 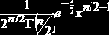  ( 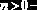 | 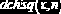 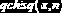 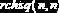 | ||
Распределение Стьюдента
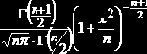 ( 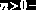 | 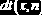 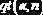 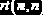 |
Функции MathCAD для вычисления квантилей распределения. Число


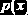
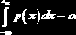
В табл. 10.1.1 в правой колонке второй строкой приведены функции MathCAD (имена начинаются с буквы

Функции MathCAD генерирования случайных векторов.
Вектор, проекции которого являются случайными числами, распределенными по определенному закону, называется случайным вектором.
В табл. 10.1.1 в правой колонке третьей строкой приведены имена функций (начинаются с буквы


Функция
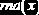
Пример 10.1.1.
На рис. 10.1.1 приведен фрагмент документа MathCAD, в котором генерируются два случайных вектора:



Функции MathCAD вычисления выборочных значений числовых характеристик. К числовым характеристикам случайной величины относятся: математическое ожидание (или среднее), дисперсия, среднеквадратическое отклонение и т.д. Часто возникает необходимость оценить эти характеристики по выборке значений случайной величины объема

Рис. 10.1.1. Моделирование и обработка статистических данных
В табл. 10.1.2 приведены имена функций, вычисляющих выборочное значение часто используемых числовых характеристик. Здесь



Таблица 10.1.2
|
Числовые характеристики |
Функция MathCAD |
Математическое ожидание случайной величины  |
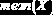 |
Дисперсия случайной величины  |
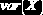 |
|
Среднеквадратическое отклонение случайной величины  |
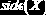 |
Медиана случайной величины  |
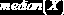 |
Мода случайной величины  |
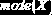 |
|
Корреляционный момент двух случайных величин  |
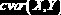 |
Пример 10.1.2.
На рис. 10.1.1 приведен фрагмент документа MathCAD, в котором вычисляются выборочные значения некоторых характеристик по выборкам, полученным в примере 10.1.1. ¦
функции MathCAD вычисления частот значений случайной величины (построение гистограмм). Введём некоторые определения.
Предположим, что дана выборка
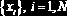

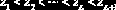
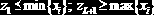
Тогда число значений

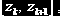
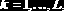

Очевидно, что
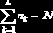
Величину
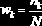
назовём относительной частотой, для которой выполняется условие
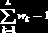
В качестве оценки плотности распределения вероятности непрерывной случайной величины Х используют гистограмму относительных частот, т.е. систему прямоугольников, k-й из которых основанием имеет
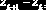

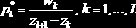
и имеет место приближенное тождество
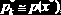
где

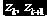
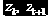
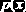
Возникает вопрос: как сформировать интервалы
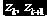
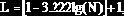
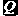

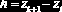

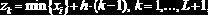
где
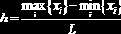
Значения wk,



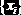
Параметры функции hist(int,X):

– массив длины (L+1), составленный из значений
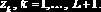
задать целым числом, равным числу интервалов L, то при выполнении функции формируется рабочий массив узлов
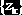

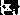
Результатом
работы функции является одномерный массив
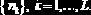
Параметры функции histogram(int,X):

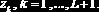
задать целым числом, равным числу интервалов L, то при выполнении функции формируется рабочий массив узлов
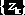

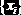
Результатом
работы функций является матрица размером

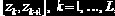

На наш взгляд, более предпочтительной является функция histogram, так как значения

Пример 10.1.3. Построить гистограммы относительных частот по выборкам случайных величин
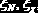
На рис. 10.1.2 показано построение гистограммы для случайной величины
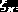


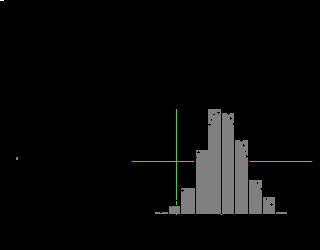
Рис. 10.1.2. Гистограмма выборки с нормальным распределением
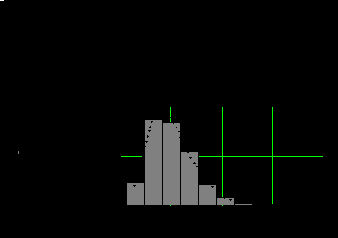
Рис. 10.1.3. Гистограмма выборки с