Построение эмпирических зависимостей

Эмпирические зависимости. В научных и инженерных исследованиях часто возникает задача математического описания некоторого исследуемого процесса или объекта. Для определенности предположим, что связь независимой переменной

 и зависимой переменной  выражается в общем случае нелинейной функций . Функция  является неизвестной, но значения переменных  могут быть измерены и результаты таких измерений представлены таблицей , где , погрешности измерений, имеющие случайную природу.

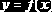
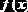
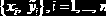
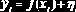
Задача построений эмпирической зависимости состоит в нахождении функции S(x), как можно точнее аппроксимирующей неизвестную f(x).

Решение этой задачи включает два этапа.

Этап 1. Выбор класса функций, из которого выбирается S(x). Например, S(x) выбирается из класса линейных функций вида S(x)=а0+а1х, где а0, а1 – параметры. Таким образом, на этом этапе эмпирическая зависимость выбирается с «точностью» до её параметров. Выбор класса функций осуществляется на основе анализа диаграммы рассеяния (в декартовой системе координат наносятся точки

) или на основе достоверной априорной информации. Например, из курса физики известно, что сопротивление металлического проводника линейно зависит от его температуры.

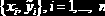
Этап 2. Вычисление неизвестных параметров функции S(x) с использованием таблицы измерений. Параметры вычисляются из условия минимума некоторого функционала F(a). Наиболее часто в качестве такого функционала используется функционал метода наименьших квадратов, имеющий вид:

                                                  (10.2.1)

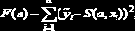
где запись S(а, x) указывает на наличие у функции S(x) параметров {aj}, j=1, 2,…, M.

Функции MathCAD для построения эмпирических зависимостей. В пакет MathCAD включены функции для вычисления параметров различных функций S(x). Обращения к этим функциям приведены в табл. 10.2.1, где Х –  вектор, составленный из значений {xi}, i=1, …, n, а Y – вектор, сформированный из значений

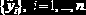
Таблица 10.2.1

Функция		Назначение функции
slope(x, y)		Вычисляет параметр а1 линейной функции
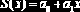intercept(x, y)		Вычисляет параметр а0 линейной функции
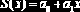regress(x,y,m)		Вычисляет параметры 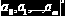 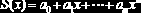полиномиальной функции для любого m (на практике 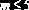). Вычисленные параметры размещаются в результирующем векторе, начиная с четвертой проекции (см. пример 10.2.2)
line(x, y)		Вычисляет параметры а0, а1 линейной зависимости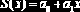
linfit (x, y,Ф)		Вычисляет параметры 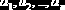 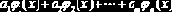линейной комбинации Базисные функции  являются проекциями вектора-функции Ф(x), формируемого до обращения к функции linfit
genfit(x,y,ао,F)		Вычисляет параметры 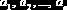 нелинейной функции S(x). До обращения формируется F(x,a) – вектор-функция размерности (m+1), составленный из самой функции S(x) и частных производных 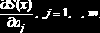 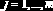ао – вектор размерности m, составленный из «стартовых» значений параметров    (см. пример 10.2.3)

<
Таблица 10.2.2

Функция	Назначение функции
expfit(X,Y,ao)	Вычисляет параметры а1, а2, а3 экспоненциальной зависимости 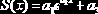. Вектор ао (размерности 3) определяет точку старта, т.е. задает «начальное» значение для а1, а2, а3
lgsfit(X,Y,ao)	Вычисляет параметры а1, а2, а3 зависимости 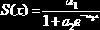. Вектор ао (размерности 3) определяет «стартовые» значения для а1, а2, а3
lnfit(X,Y)	Вычисляет параметры а1, а2 зависимости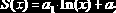
logfit(X,Y, ao)	Вычисляет параметры а1, а2, а3 зависимости 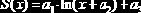.Вектор ао (размерности 3) задаёт «стартовые» значения для а1, а2, а3
pwrfit(X,Y,ao)	Вычисляет параметры степени зависимости 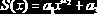. Вектор ао (размерности 3) задаёт «стартовые» значения для а1, а2, а3
sinfit(X,Y,ao)	Вычисляет параметры синусоидальной зависимости 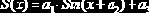. Вектор ао (размерности 3) задаёт «стартовые» значения для а1, а2, а3

 
Пример 10.2.4. По данным, приведенным на рис. 10.2.4, построить эмпирическую зависимость вида
.
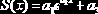
Построение этой эмпирической зависимости показано в документе MathCAD, приведенном на рис. 10.2.4. ¨

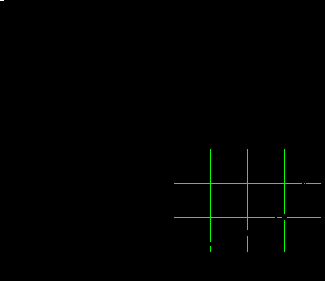
Рис. 10.2.4. Построение экспоненциальной зависимости
Приведенные в табл. 10.2.1 и 10.2.2 функции осуществляют построение эмпирических зависимостей, которые можно назвать «глобальными»,
так как при вычислении их параметров используется вся таблица исходных данных. В ряде экспериментов возникает необходимость построить эмпирическую зависимость по некоторому небольшому набору исходных данных, которые находятся в окрестности точки х, для которой будет вычисляться значение эмпирической формулы. Такие эмпирические формулы можно назвать «локальными».
Для построения «локальных» эмпирических зависимостей в MathCAD включена функция loess(X,Y,d), приближающая исходные данные полиномом второй степени. Формальные параметры X, Y – это массивы с исходными данными, а параметр  определяет размер области приближаемых данных (рекомендуемое начальное значение 0.75 – 0.85). Чем больше величина d, тем больше сглаживание исходных данных. При больших значениях d работа функции loess(X,Y,d) становится аналогичной функции regress(X,Y,2). Результатом работы функции loess(X,Y,d) является вектор v, используемый функцией interp(v,X,Y,z), которая вычисляет значение построенной эмпирической формулы в точке z.


Пример 10.2.5. На рис. 10.2. 5 приведен документ MathCAD, реализующий вычислительный эксперимент по построению локальной эмпирической формулы с помощью функции loess(X,Y,d) при  и . Из графиков видно, что формула при  достаточно хорошо приближает полином второго порядка. ¨

 
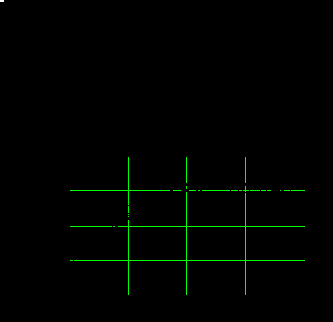
Рис. 10.2.5. Построение локальных эмпирических зависимостей
 
Сглаживание экспериментальных данных. В большинстве случаев результаты измерения содержат случайные погрешности, которые необходимо «отфильтровать». Это можно сделать путем построения эмпирических зависимостей. Однако в MathCAD определены специальные «сглаживающие» функции, имена которых содержат слово smooth (гладкий). Таких функций три:

• medsmooth(Y,m) – сглаживает массив Y, состоящий из n элементов с использованием скользящего медианного фильтра с размером окна сглаживания m (m должно быть нечетным и
  
  ). Результатом работы является массив, содержащий n сглаженных значений массива Y;


• supsmooth(X,Y) – сглаживает массив Y, состоящий из n значений, измеренных в точках
  
  , которые являются элементами массива X. Сглаживание осуществляется построением линейной регрессии по k – ближайшим точкам
  
  с адаптивным выбором «размера» k
  окна сглаживания. Элементы массива X должны быть упорядочены по возрастанию;


• ksmooth(X,Y,b) – сглаживает массив Y, состоящий из n значений, измеренных в точках
  
  , которые являются элементами массива X. Сглаживание осуществляется на основе формулы



, где

.
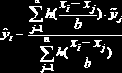
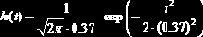
Видно, что сглаженное значение

 есть сумма измерений

 с экспоненциальными весами, величина которых зависит от параметра

 – чем больше величина параметра, тем в большей степени сглаживаются «зашумленные» значения

.
Пример 10.2.6. На рис. 10.2.6 приведен документ MathCAD, реализующий вычислительный эксперимент по сглаживанию «зашумленных» данных (относительный уровень шума равен 38%) с помощью функции ksmooth при двух значениях параметра

 (

=0.3 – относительная ошибка сглаживания равна 0.161 и

=0.9 – относительная ошибка сглаживания равна 0.141).





 
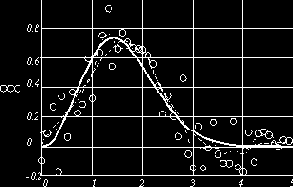
Рис. 10.2.6. Сглаживание данных функций ksmooth

ЗАКЛЮЧЕНИЕ
В данном пособии авторы стремились изложить основы программирования в пакете MathCAD и продемонстрировать решение часто встречающихся задач в этом пакете. К сожалению, ограниченный объем учебного пособия не позволил уделить внимание ряду важных возможностей пакета. Это прежде всего относится к символьным вычислениям, к решению обыкновенных дифференциальных уравнений и дифференциальных уравнений в частных производных. Некоторым «оправданием» служит хорошее освещение этих тем в литературе [ 2, 3, 9,10 ].
Авторы желают читателям (особенно студентам и аспирантам), чтобы пакет MathCAD стал для них «дружелюбным и незаменимым» помощником в решении широкого круга научно-инженерных задач.
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
 
1.        Дьяконов В.П. Компьютерная математика. Теория и практика / В.П. Дьяконов. – М.: Изд-во Нолидж, 2001. – 296 с.
2.        Дьяконов В.П. MathCAD2000: Учебный курс / В.П. Дьяконов. – СПб: Питер, 2000. – 596 с.
3.        Дьяконов В.П. MathCAD 8 Professional в математике, физике и Internet / В.П. Дьяконов, И.В. Абраменконова. – М.: Нолидж, 1999. – 512 с.
4.        Дьяконов В.П. Matlab: Учебный курс / В.П. Дьяконов. – СПб: Питер, 2001. – 560 с.
5.        Потемкин В.Г. Система инженерных и научных расчетов Matlab 5.x.: В 2-х т. – М. ДИАЛОГ–МИФИ, 1999. – 672 с.
6.        Дьяконов В.П. Mathematica 4: Учебный курс / В.П. Дьяконов. – СПб: Питер, 2000 – 482 с.
7.        Дьяконов В.П. Математическая система Maple V R3/R4/R5 / В.П. Дьяконов. – М.: Солон, 1998. – 381 с.
8.        Воскобойников Ю.Е. Программирование в математическом пакете MathCAD. Методические указания / Ю.Е. Воскобойников, Т.Н. Воскобойникова. – Новосибирск: Изд-во НГАСУ, 1999. – 32 с.


9.        Кирьянов Д.В. Самоучитель MathCAD2001 / Д.В. Кирьянов. – СПб.: БХВ-Петербург, 2002. – 459 с.
10.    Очков В.Ф. Советы пользователям Mathcad / В.Ф. Очков. – М.: Изд-во МЭИ, 2001. – 196 с.
11.    Демидович В.П. Основы вычислительной математики / В.П. Демидович, И.А. Марон. – М.: Наука, 1970. – 486 с.
СОДЕРЖАНИЕ
 
ВВЕДЕНИЕ        5
РАЗДЕЛ 1. Экспорт и импорт данных в пакете          MathCAD      7
Тема 1. Запись и чтение файловых данных     7
1.1. Файловый тип данных MathCAD................................. 7
1.2. Запись данных в файл.................................................. 9
1.3. Чтение данных из файла............................................ 13
Тема 2. Обмен информацией с другими прОграммами-приложениями       15
2.1. Обмен информацией с текстовым процессором Word 15
2.2. Обмен информацией с табличным процессором Excel 19
РАЗДЕЛ 2. ПРОГРАММИРОВАНИЕ В ПАКЕТЕ MathCAD          27
ТЕМА 3. БЕЗМОДУЛЬНОЕ ПРОГРАММИРОВАНИЕ В ПАКЕТЕ MathCAD   28
3.1. Программирование линейных алгоритмов............... 28
3.2. Программирование разветвляющихся алгоритмов.. 29
3.3. Программирование циклических алгоритмов.......... 35
ТЕМА 4. ПОДПРОГРАММА-ФУНКЦИЯ: ОПИСАНИЕ                            И ВЫЗОВ   39
4.1. Описание подпрограммы-функции и локальный оператор присваивания    39
4.2. Обращение к подпрограмме-функции Mathcad...... 42
ТЕМА 5. Программирование АЛГОРИТМОВ в ПОДпрограмме-функции MathCAD         44
5.1. Программирование линейных алгоритмов в подпрограмме-функции         44
5.2. Программирование разветвляющихся алгоритмов в подпрограмме-функции        45
5.3. Программирование циклических алгоритмов в подпрограмме-функции     51
ТЕМА 6. Программирование типовых задач в подпрограммах-функциях mathCAD         62
6.1. Программирование разветвляющихся алгоритмов.. 62
6.2. Программирование циклов типа арифметической прогрессии         66


6.3. Программирование итерационных циклов............... 74
ТЕМА 7. МОДУЛЬНОЕ ПРОГРАММИРОВАНИЕ В MathCAD    80
7.1. Преимущества модульного программирования....... 80
7.2. Модульное программирование в пределах одного документа MathCAD    81
7.3. Модульное программирование в нескольких документах MathCAD           84
7.4. Программы MathCAD в Internet................................. 85
РАЗДЕЛ 3. РЕШЕНИЕ НАУЧНО-ИНЖЕНЕРНЫХ ЗАДАЧ В ПАКЕТЕ MathCAD  94
ТЕМА 8. РЕШЕНИЕ НЕЛИНЕЙНЫХ УРАВНЕНИЙ И СИСТЕМ В ПАКЕТЕ MathCAD         94
8.1. Решение нелинейных уравнений............................... 94
8.2. Решение систем уравнений...................................... 105
ТЕМА 9. Решение оптимизационных задач в пакете MathCAD       112
9.1. Решение оптимизационных задач без ограничений 112
9.2. Решение оптимизационных задач с ограничениями 114
ТЕМА 10. ОБРАБОТКА ЭКСПЕРиМЕНТАЛЬНЫХ ДАННЫХ В ПАКЕТЕ MathCAD         118
10.1. Моделирование и обработка статистических              данных        118
10.2. Построение эмпирических зависимостей............. 125
Заключение         135
БИБЛИОГРАФИЧЕСКИЙ СПИСОК     135
        
 

Содержание раздела



---





---

---

Главная сайта

---