Программирование циклических алгоритмов вподпрограмме-функции
Напомним, что циклические алгоритмы (циклы) содержат повторяющиеся вычисления, зависящие от некоторой переменной. Такая переменная называется параметром цикла, а сами повторяющиеся вычисления составляют тело цикла. Циклы можно условно разделить на две группы:
· циклы типа арифметической прогрессии;
· итерационные циклы.
Особенности этих циклов были рассмотрены в п. 3.3.
Программирование цикла типа арифметической прогрессии. Для программирования таких циклов используется оператор цикла for (часто называемый оператором цикла с параметром). Для ввода такого оператора необходимо выполнить следующие действия:
- щелкнуть на кнопке for палитры ПрограммированиЕ. На экране появятся поля ввода, изображенные на рис. 5.3.1;
 |
Рис. 5.3.1. Поля оператора цикла for
· в поле ввода 1 ввести имя переменной, являющейся параметром цикла;
· в поле 2 — закон изменения параметра цикла, используя для этого описание дискретной переменной или описание массива;
· в поле 3 — операторы, составляющие тело цикла. Если одной строки недостаточно, то дополнительные поля ввода (дополнительные строки) создаются щелчком на кнопке Add line палитры программированиЕ, и тогда слева от тела цикла появляется вертикальная черта, охватывающая тело цикла.
Пример 5.3.1. Составить описание П-Ф, реализующей алгоритм примера 3.3.1.
Описание П-Ф и ее вызов приведены на рис. 5.3.2. Заметим, что значение системной переменной ORIGIN (начальное значение индексного выражения) задается равным 1. ¨

Рис. 5.3.2. Подпрограмма-функция формирования вектора
Пример 5.3.2.
Для x меняющегося от -2 до 2 с шагом 0.5 вычислить значение f(x) = e-x. Cos (2x) и сформировать из этих значений вектор y, т.е. y1 = f(-2), y2 = f(-1.5) и т.д.
В этом примере количество повторений тела цикла определяется по формуле
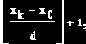 |
где xk, x0
– конечное и начальное значения параметра цикла, d – шаг его изменения. Подставив значения, получаем (2–(–2))/0.5+1=9. Следовательно, сформированный вектор y будет содержать 9 элементов. Необходимо отметить, что алгоритм формирования содержит два параметра цикла: первый параметр – переменная x, определяющая текущее значение аргумента функции f(x); второй – это переменная i, определяющая текущее значение индекса у элемента формируемого вектора. Но между этими двумя параметрами имеется однозначное соответствие, поэтому цикл нужно организовывать только по одному параметру, например, по переменной x, а значение второго параметра будет вычисляться в теле цикла.
Описание П-Ф и ее вызов приведены на рис. 5.3.3. Видно, что в теле цикла выполняется два оператора. Первый оператор формирует элемент массива y, а второй изменяет на 1 значение индекса. ¨

Рис. 5.3.3. Формирование вектора примера 5.3.2
Пример 5.3.3. Составить описание П-Ф, где значения параметра цикла задаются вектором.
На рис. 5.3.4 приведено описание такой П-Ф.
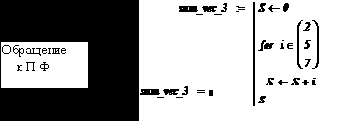

Рис. 5.3.4. Описание П-Ф примера 5.3.3
Задание 5.3.1. Составьте описание П-Ф формирования вектора y примера 5.3.2, приняв в качестве параметра цикла переменную i.
Программирование итерационных циклов. Для программирования таких циклов используется оператор цикла while. Для ввода этого оператора необходимо выполнить следующие действия:
· щелкнуть на кнопке while палитры ПрограммированиЕ. На экране появляются элементы, показанные на рис. 5.3.5;
Рис. 5.3.5. Структура оператора цикла while
· в поле 1 ввести условие выполнения цикла;
· в поле 2 ввести операторы тела цикла. В теле цикла должны присутствовать операторы, которые могут изменить значение условия цикла, иначе цикл будет продолжаться бесконечно.
Оператор цикла while выполняется следующим образом: обнаружив оператор while, Mathcad проверяет указанное в операторе условие. Если оно равно 1 (т.е. выполняется), то выполняется тело цикла, и снова проверяется условие. Если условие принимает значение 0, то цикл заканчивается.
Пример 5.3.4. Составим П-Ф, реализующую итерационную процедуру приближенного вычисления корня квадратного, описанную в примере 3.3.2. Описание П-Ф приведено на рис. 5.3.6.
Как видно из текста, П-Ф нет необходимости хранить в памяти все приближенные решения x0, x1, x2,... (как это делалось при использовании функции until — см. рис. 3.3.3). Достаточно хранить предыдущее («старое») значение (обозначим его как xc) и последующее («новое») значение xn.
К сожалению, организация итерационного цикла с помощью оператора while без дополнительных средств контроля может привести к зацикливанию, т.е. повторению тела цикла «бесконечное» число раз. Например, задав при обращении к П-Ф

Вызов подпрограммы-функции
 |

Рис. 5.3.6. Реализация итерационного цикла примера 5.3.4
Поэтому в Mathcad имеется специальный оператор break, который позволяет выйти из цикла или приостановить исполнение программы при выполнении заданного в операторе break условия. Для ввода оператора break необходимо щелкнуть на кнопке break панели ПрограммированиЕ (нельзя вводить этот оператор с клавиатуры по символам). Оператор break используется в левом поле ввода условного оператор if, а в правом размещается условие, при выполнении которого происходит прекращение работы цикла или программы. Поэтому первоначально вводится оператор if, а затем заполняются поля этого оператора. Следующий пример показывает написание подпрограммы без «зацикливания» с использованием оператора break.
Пример 5.3.5. Составим П-Ф, реализующую итерационную про цедуру вычисления корня квадратного без «зацикливания». Описание П-Ф приведено на рис. 5.3.7.
В этой подпрограмме число повторений тела ограничено 10000. Если за это число итераций приближенное значение корня с заданной точностью не найдено, то параметр ierr – индикатор ошибки получает значение 1, что говорит об ошибке в вычислительном процессе. Для передачи двух вычисленных значений xn, ierr используется вектор. Если ierr = 1, то переменной xn присваивается значение строковой константы “not solve” для привлечения внимания пользователя к ошибочному завершению работы П-Ф. Заметим, что после обращения к П-Ф необходимо обязательно проверить значение индикатора ошибки ierr и, в зависимости от его значения, либо продолжить работу с вычисленным значением корня квадратного, либо прекратить дальнейшие вычисления и определить причину появления ошибки. ¨
Вызов подпрограммы-функции
 |

Рис. 5.3.7. Реализация итерационного цикла без «зацикливания»
Пример 5.3.6. Составить П-Ф, осуществляющую суммирование ряда с бесконечным числом слагаемых. Накопление суммы прекращается, как только очередное слагаемое по абсолютной величине становится меньше заданной погрешности

Описание П-Ф и ее вызов показаны на рис. 5.3.8. Заметим, что вторым формальным параметром является имя функции пользователя, определяющей зависимость величины члена ряда от его номера. При вызове этот формальный параметр заменяется фактическим – именем функции пользователя, описанной до обращения к П-Ф. ¨

 |
|
Описание слагаемых суммируемых рядов |
