Программирование циклов типа арифметическойпрогрессии

                В этом параграфе будут рассмотрены четыре типа циклических алгоритмов, входящих в более сложные алгоритмы. Во всех ниже приведенных фрагментах MathCAD системная переменная ORIGIN=1.

                          Тип 1 (формирование  элементов массива,

                          удовлетворяющих  заданным условиям)

Пример 6.2.1. Составить П-Ф, формирующую матрицу a по следующему правилу:

                

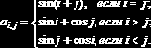
Описание П-Ф приведено на рис. 6.2.1.  ¨

 

Рис. 6.2.1. Реализация алгоритма примера 6.2.1

Задание 6.2.1. Даны два вектор x и

y, состоящие из  n элементов. Составить П-Ф, формирующую матрицу B

размерности 

 по следующему правилу:

                   

   

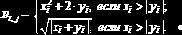
Задание 6.2.2. Даны два вектора x и

y, состоящие из  n элементов. Составить П-Ф, формирующую вектор q размерности n,  i-й элемент которого равен 1, если точка с координатами

принадлежит кругу  радиуса  r с центром в начале координат.  ?

Задание 6.2.3. Дана матрица A размерности

. Составить П-Ф, заменяющую все элементы матрицы, с четной суммой индексов на 1, а другие элементы – на 0. ?

Задание 6.2.4. Даны два вектора x, y, состоящие из n  элементов. Преобразовать эти векторы по правилу: большее из чисел xi и yi принять в качестве нового значения xi, а меньшее – в качестве нового значения yi. ?

Тип 2 (подсчет числа элементов массива или

последовательности, удовлетворяющих  заданным условиям)

            Пример

6.2.2. Дан массив y, состоящий из n элементов. Составить П-Ф, определяющую:

• число элементов, удовлетворяющих условию  
  
  ;
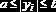
• число положительных элементов.  

      Описание П-Ф приведено на рис. 6.2.2.   ¨

Пример 6.2.3. Дана квадратная матрица С размерности


. Составить П-Ф, вычисляющую число элементов, находящихся ниже главной диагонали и удовлетворяющих условию 

. Заметим, что для элементов, лежащих ниже главной диагонали справедливо неравенство

. Поэтому возможны два варианта выбора элементов, лежащих ниже главной диагонали: а) проверять все элементы матрицы на выполнение этого условия; б) организовать двойной цикл так, чтобы в нем было обращение только к элементам, удовлетворяющим этому условию. В П-Ф, приведенной на рис. 6.2.3 реализован второй вариант. ¨

          


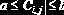
              Рис. 6.2.2. Реализация алгоритма примера 6.2.2
           


              Рис. 6.2.3. Реализация алгоритма примера 6.2.3
            Пример 6.2.4. Дана последовательность
                

  где  i=1,2,...,n;  n=10.
Составить П-Ф, подсчитывающую число отрицательных членов последовательности и число членов, принадлежащих отрезку [0.5, 1].
При составлении описания учтем два момента: а) для универсальности П-Ф элементы последовательности задаются  функцией пользователя, имя которой будет параметром П-Ф; б) для подсчета числа элементов необязательно внутри П-Ф формировать массив из элементов последовательности – достаточно работать со значением текущего элемента последовательности. Описание П-Ф  и ее вызов приведены на рис. 6.2.4. ¨











                    


Рис. 6.2.4. Реализация алгоритма примера 6.2.4
Пример 6.2.5. Дана матрица D размерности

. Составить П-Ф, формирующую вектор, i-й элемент которого  равен количеству положительных элементов в  i-й строке матрицы D. Описание П-Ф  приведено на рис. 6.2.5. Здесь (в отличие от предыдущего примера) искомая характеристика (количество положительных элементов) вычисляется для каждой строки матрицы. Поэтому нулевое начальное значение задается в теле  внешнего цикла до начала внутреннего  цикла. ¨











                       


Рис. 6.2.5. Реализация алгоритма примера 6.2.5
            Задание 6.2.4. Даны две матрицы A, B размерности

. Составить  П-Ф,  подсчитывающую число случаев  

   ?
Задание 6.2.5. Дана матрица D размерности

. Составить П-Ф, которая вместо последнего элемента i-й строки записывает  количество элементов  i-й строки матрицы D, удовлетворяющих условию

, где

 – задаваемая величина. ?
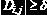
                          Тип 3 (подсчет суммы или произведения
    элементов массива,  удовлетворяющих  заданным условиям)
            Пример 6.2.6. Дан массив y, состоящий из n элементов. Составить П-Ф, определяющую:

• произведение строго положительных элементов массива;




• сумму элементов, находящихся в интервале 
  
  .     

Описание П-Ф приведено на рис. 6.2.6. Обратите внимание, что начальные значения для переменных sum, pr
задаются до начала цикла, в котором происходит «накопление» значений этих переменных. ¨
   


     Рис. 6.2.6. Реализация алгоритма примера 6.2.6
Пример 6.2.7. Дана матрица A размерности

. Составить П-Ф, которая вместо первого элемента i-й строки записывает сумму всех элементов этой строки матрицы. Описание П-Ф  приведено на рис. 6.2.7.
Задание 6.2.6. Дан вектор x, состоящий из n элементов. Составить П-Ф, вычисляющую наибольшую из двух сумм элементов с четными и нечетными индексами. ?
Задание 6.2.7. Дан вектор x, состоящий из n
элементов. Составить П-Ф, вычисляющую среднее арифметическое элементов вектора, а затем преобразующую исходный вектор  по правилу: те элементы, которые меньше среднего арифметического, заменить нулями. ?











                             


         Рис. 6.2.7. Реализация алгоритма примера 6.2.7
Задание 6.2.8. Дана матрица A размерности

. Составить П-Ф, формирующую вектор,  i-й элемент равен среднему арифметическому  i-й строки матрицы. ?
Задание 6.2.9. Дана матрица A размерности

. Составить П-Ф, вычисляющую сумму и количество только тех элементов матрицы, которые удовлетворяют условию

, где

— задаваемая величина.  ?
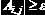
Задание 6.2.10. Имеется экзаменационная ведомость студенческой группы из n = 20 человек по m = 5 дисциплинам. Оценки из этой ведомости занесены в матрицу размерности

. Составить П-Ф, вычисляющую число студентов, получивших только четверки и пятерки. ?
Задание 6.2.11. Имеется экзаменационная ведомость студенческой группы из n = 20 человек по m = 5 дисциплинам. Оценки из этой ведомости занесены в матрицу размерности

. Составить П-Ф, вычисляющую средний балл по каждой дисциплине. ?
             Тип 4 (вычисление максимального или минимального
                            элемента массива и его индекса)


            Пример 6.2.8. Дан массив y, состоящий из n элементов. Составить П-Ф, меняющую максимальный и минимальный элемент местами. Описание П-Ф приведено на рис. 6.2.8.  ¨    










     
Рис. 6.2.8. Реализация алгоритма примера 6.2.8
Пример 6.2.9. Дана функция f(x) и вектор x,  состоящий из  n  элементов. Составить описание П-Ф, определяющей: а) максимальное значение этой функции на элементах этого  вектора; б) номер индекса и значение элемента массива, на котором функция достигает максимального значения.
Описание П-Ф  и обращение к ней приведены на рис. 6.2.9. Заметим, что в качестве третьего параметра П-Ф используется имя функции пользователя. Формальным параметром является функция f(x), а фактическим — функция

, описание которой должно находиться до обращения  к П-Ф.  ¨
Пример 6.2.10. Дана матрица A размерности

. Составить П-Ф, формирующую вектор,  i-й элемент равен номеру столбца в котором на   i-й строке матрицы стоит минимальный элемент. Описание П-Ф приведено на рис. 6.2.10.   ¨















                


Рис. 6.2.9. Реализация алгоритма примера 6.2.9











                                  


              
Рис. 6.2.10. Реализация алгоритма примера 6.2.10
Задание 6.2.12. Даны две матрицы A, B размерности

. Вычислить величину

, где

 

максимальные значения матриц A, B соответственно. Для вычисления значения максимального элемента составить П-Ф. ?
Задание 6.2.13.  Дана матрица A размерности

. Составить П-Ф, меняющую местами максимальный и минимальный элементы матрицы. ?
Задание 6.2.14. Дана матрица A размерности

. Составить П-Ф, вычисляющую  номер столбца, который содержит наименьший по модулю элемент этой матрицы. ?
Задание 6.2.15. Имеется экзаменационная ведомость студенческой группы из n = 20 человек по m = 5 дисциплинам. Оценки из этой ведомости занесены в матрицу размерности

. Составить П-Ф, вычисляющую номер дисциплины (т.е. номер столбца), имеющей максимальный средний балл.  ?
Задание 6.2.16. Имеется экзаменационная ведомость студенческой группы из n = 15 человек по m = 4 дисциплинам. Оценки из этой ведомости занесены в матрицу размерности

. Составить П-Ф, вычисляющую номер студента (т.е. номер строки), имеющего максимальный средний балл по учебным дисциплинам.  ?

Содержание раздела



---





---

---

Главная сайта

---