Программирование итерационных циклов

Пример 6.3.1. Составить описание П-Ф, вычисляющей факториал числа

по формуле

Описание П-Ф с использованием оператора произведения приведено на рис. 6.3.1.

Рис. 6.3.1. Вычисление факториала числа

Описание П-Ф с использованием итерационного цикла и оператора break приведено на рис. 6.3.2. Обратите внимание на запись условия в операторе while, а именно while 1, что обеспечивает повторение тела цикла до тех пор, пока не выполнится условие n = 1, что приведет к выполнению оператора break и выходу из цикла. ¨

Рис. 6.3.2. Вычисление факториала числа

Пример 3.6.2. Дан вектор v, состоящий из n элементов. Составить П-Ф, определяющую первый элемент этого массива, который удовлетворяет условию

, где

— заданные величины.

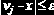
Описание П-Ф приведено на рис. 6.3.3. Эту же задачу можно реализовать с помощью оператора цикла for, что предотвратит «зацикливание», которое может иметь место в П-Ф search при неправильном задании исходных данных (например, при задании

). Описание П-Ф приведено на рис. 6.3.4. ¨

Рис. 6.3.3. Реализация алгоритма примера 6.3.2

Рис. 6.3.4. Реализация алгоритма примера 6.3.2

В двух предыдущих примерах была показана возможность замены оператора while (используемого при программной реализации итерационного цикла) другими конструкциями. Это обусловлено тем, что в этих примерах параметры цикла изменялись по закону арифметической прогрессии. Однако встречаются циклы, параметры которых изменяются по более сложным соотношениям. Особенно это характерно для алгоритмов решения нелинейных уравнений. В примере 6.3.3 рассматривается один из таких алгоритмов – метод последовательных предложений.

Пример 6.3.3. Дано нелинейное уравнение

. (6.3.1)

Необходимо вычислить с точностью

вещественный корень, лежащий в интервале

, используя метод последовательных приближений (называемый также методом простой итерации). Не останавливаясь на теоретическом обосновании, приведем основные расчетные соотношения, необходимые для программной реализации этого метода.
Первоначально исходное уравнение

заменяется эквивалентным ему уравнением

. (6.3.2)
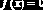
Затем выбираем начальное значение

из некоторого интервала

, внутри которого находится только один корень уравнения

(в нашем примере это интервал

). Подставляя это значение в правую часть (6.3.2), получаем первое приближение

. Затем значение

вновь подставляем в правую часть (6.3.2) и получаем

.
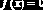
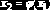
Повторяя этот процесс, получаем последовательность чисел

(6.3.3)
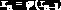
(это оправдывает название – метод последовательных приближений). Возможны два случая.
Случай 1. Последовательность

сходится к некоторому числу

, т.е. имеет предел, и тогда этот предел является решением нелинейного уравнения, т.е.

.
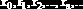
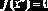
Случай 2. Последовательность

расходится,
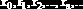
т.е. не имеет предела, и в этом случае метод не применим.
Приведем условие, являющееся достаточным для сходимости метода последовательных приближений.
Пусть на отрезке

имеется единственный корень уравнения

, и во всех точках этого отрезка справедливо неравенство

. (6.3.4)
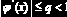
Если при этом выполняется и условие

, (6.3.5)
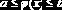
то итерационный процесс (6.3.3) сходится, а за нулевое приближение можно брать любое

.
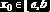
Заметим, что чем меньше величина q в (6.3.4), тем быстрее сходится последовательность

к своему пределу

. В качестве приближенного значения корня можно принять приближение

, удовлетворяющее условию

, (6.3.6)
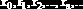
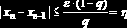
где

— заданная точность вычисления корня, входящая в неравенство

, (6.3.7)

— точное значение корня.
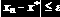
Вернемся к уравнению нашего примера и преобразуем его к виду (6.3.2). Получаем

(знак минус появился из-за отрицательности искомого корня), т.е.

. Проверим выполнение условия (6.3.4) графическим способом, используя графику MathCAD (см. рис. 6.3.5).

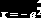
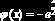
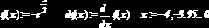
Рис. 6.3.5. Проверка условия (6.3.4)
Из графика видно, что в качестве величины

в условии (6.3.4) можно принять значение 0.5, которое удовлетворяет условию (6.3.4).
Для проверки условия (6.3.5) построим график функции

на интервале

(см. рис. 6.3.6). Видно, что условие (6.3.5) также выполняется – на всем интервале

функция

удовлетворяет условию

.
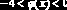
Вывод: метод последовательных приближений для любого

сходится к точному решению нелинейного уравнения (6.3.1).

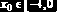
Определим величину

в условии окончания итераций (6.3.6):

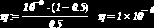
Описание П-Ф, реализующей метод последовательных приближений приведено на рис. 6.3.7. Здесь же показаны вычисленное приближенное значение корня и его проверка. Имя функции

является формальным параметром. Для предотвращения «зацикливания» итерационной процедуры (6.3.3) используется оператор цикла for (обсуждение см. в примере 5.3.4). Заметим, что переменные

, используемые в теле П-Ф, являются простыми переменными, имена которых имеют нижние индексы (вводимые после нажатия клавиши

– «десятичная точка»). ¨

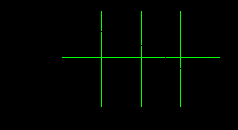
Рис. 6.3.6. Проверка условия (6.3.5)

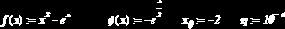
Рис. 6.3.7. Программная реализация метода
последовательных приближений
Задание 6.3.1. Дано нелинейное уравнение

.
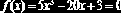
Составьте П-Ф для вычисления корня уравнения, лежащего в интервале

, методом последовательных приближений. Для организации итерационного цикла используйте оператор цикла while (см. пример 5.3.3). ?
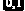
Задание 6.3.2. Дано нелинейное уравнение

.
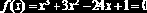
Составьте П-Ф для вычисления двух корней уравнения, лежащих в интервалах [–7, –1] и [2, 12], методом последовательных приближений с точностью 0.001. Для организации итерационного цикла используйте оператор цикла while (см. пример 5.3.3). ?

Содержание раздела