Уточнение корней нелинейного уравнения

Под уточнением корня подразумевают процедуру уменьшения длины интервала локализации таким образом, чтобы корень уравнения всегда находился в новом интервале локализации (обозначим такой интервал локализации как

). Процедура уточнения завершается, если выполняется условие

,                                                                  (8.1.7)

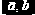
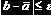
где

 – заданная точность вычисления корня. Для уточнения корня используются специальные вычислительные методы [11] такие, как метод деления отрезка пополам, метод хорд, метод касательных (метод Ньютона) и многие другие.

 

Пример 8.1.3.

Используя метод деления отрезка пополам, уточнить корни уравнения (8.1.5). Реализовать метод в виде П-Ф.

Метод деления отрезка пополам заключается в делении длины «старого» интервала локализации пополам и принятии в качестве «нового» интервала локализации

 такого интервала из двух полученных, у которого на концах функция имеет разные знаки, т.е. .

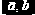
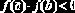
Описание П-Ф root_2 приведено на рис. 8.1.4. Здесь же показаны уточненные значения корней. Выполненная проверка показала высокую точность нахождения корней.

                                              

Рис. 8.1.4. Реализация метода «деления отрезка пополам»

Заметим, что в теле П-Ф для организации итерационного цикла использовался оператор цикла for, что предотвращает «зацикливание» при неправильно заданных исходных данных. ¨

Функция root. В MathCAD для уточнения корней любого нелинейного уравнения (не обязательно только алгебраического) введена функция root, которая может иметь два или четыре аргумента, т.е.

 или , где  – имя функции или арифметическое выражение, соответствующее решаемому нелинейному уравнению,  – скалярная переменная, относительно которой решается уравнение,  – границы интервала локализации корня.

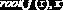
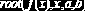
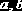
Пример 8.1.4.

Используя функцию

, найти все три корня уравнения (8.1.6), включая и два комплексных (см. пример 8.1.2). Фрагмент документа MathCAD, вычисляющий эти корни приведен на рис. 8.1.5.

 
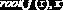
Рис. 8.1.5. Вычисление корней уравнения примера 8.1.2
Заметим, что для вычисления всех трех корней
использовался прием понижения порядка алгебраического уравнения, рассмотренный в п. 8.1.1. ¨
Функция root с двумя аргументами требует задания (до обращения к функции) переменной  начального значения корня из интервала локализации.
 Рекомендации по использованию функции root:

• в функции root реализован метод секущих [11], поэтому требуется предварительная локализация корней решаемого нелинейного уравнения;


• для изменения точности, с которой функция root ищет корень, нужно изменить значение системной переменной TOL. Если значение TOL увеличивается, функция root будет сходиться быстрее, но ответ будет менее точен. Если значение TOL уменьшается, то функция root будет сходиться медленнее, но ответ будет более точен. Чтобы изменить значение TOL в определенной точке документа MathCAD, используйте определение вида
  
  . Чтобы изменить значение TOL для всего рабочего документа, необходимо обратиться к пункту меню Математика команда Опции в появившемся диалоговом окне в закладке Встроенные переменные изменить значение системной переменной TOL (по умолчанию она равна 0.001);


• если два корня расположены близко друг от друга, следует уменьшить TOL, чтобы различить их;


• если функция f(x) имеет малый наклон около искомого корня, функция root(f(x), x) может сходиться к значению r, отстоящему от корня достаточно далеко. В таких случаях для нахождения более точного значения корня необходимо уменьшить значение TOL. Другой вариант заключается в замене уравнения f(x) = 0 на эквивалентное g(x) = 0, где



.
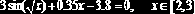
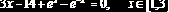
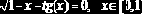
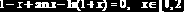
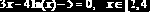
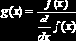
Пример 8.1.5.
Используя функцию root, вычислить изменения корня нелинейного уравнения

при изменении коэффициента а от 1 до 10 с шагом 1.
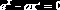
Фрагмент документа приведен на рис. 8.1.6. ¦



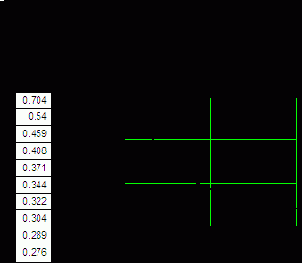
Рис. 8.1.6. Вычисление корней уравнения в цикле
Функция polyroots. Для вычисления всех корней алгебраического уравнения вида (8.1.2) порядка

(не выше 5) рекомендуется использовать функцию polyroots. Обращение к этой функции имеет вид polyroots(v), где v – вектор, состоящий из n +1 проекций, равных коэффициентам алгебраического уравнения, т.е.

. Эта функция не требует проведения процедуры локализации корней.


Пример 8.1.6.
Используя функцию polyroots, найти все три корня уравнения (8.1.6), включая и два комплексных (см. пример 8.1.2). Фрагмент документа MathCAD, вычисляющий эти корни приведен на рис. 8.1.7. ¦
Задание 8.1.1. Используя функцию root, вычислить корень из указанного интервала локализации следующих нелинейных уравнений:

• 
  ;


• 
  . ?




Рис. 8.1.7. Вычисление корней уравнения
с использованием функции polyroots
Блок Given. При уточнении корня нелинейного уравнения можно использовать специальный вычислительный блок Given, имеющий следующую структуру:


                                                           (8.1.8)
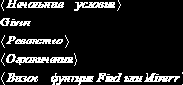
Решаемое уравнение задается в виде равенства, в котором используется «жирный» знак равно, вводимый с палитры Логичес­кий. Ограничения содержат равенства или неравенства, которым должен удовлетворять искомый корень.
Функция Find уточняет корень уравнения, вызов этой функции имеет вид Find(x), где x – переменная, по которой уточняется корень. Если корня уравнения на заданном интервале не существует, то следует вызвать функцию Minerr(x), которая возвращает приближенное значение корня.
Для уточнения корней в функциях Find(x), Minerr(x) реализованы различные численные алгоритмы и пользователю предоставляется возможность либо задать один из реализованных алгоритмов (к которому он имеет «максимальное доверие»), либо предоставить право выбора алгоритма пакету MathCAD. Для этого необходимо щелкнуть правой кнопкой мыши на имени функции Find(x) и в появившемся контекстном меню (см. рис. 8.1.8) выбрать подходящий алгоритм. Пользователю, не «искушенному» в вычислительных методах рекомендуется предоставить выбор MathCAD, включив для этого команду Автовыбор. В контекстном меню можно увидеть выбранный алгоритм.





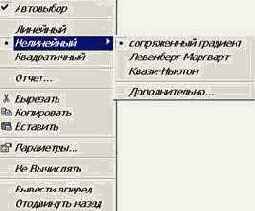
Рис. 8.1.8. Задание алгоритма функции Find
Аналогично можно задать алгоритм решения и для функции Minerr(x).
Замечание 8.1.1. Использование численных методов в функциях Find(x), Minerr(x) требует перед блоком Given задать начальные значения переменным, по которым осуществляется поиск корней уравнения.


Пример 8.1.7. Используя блок Given, вычислите корень уравнения примера 8.1.2 в интервале отделения

. Фрагмент документа приведен на рис. 8.1.9. ¨
Задание 8.1.2. Используя блок Given, вычислить корень из указанного интервала отделения следующих нелинейных уравнений и выполнить проверку найденных корней:

• 
  ;


• 
  ;


• 
  . ?








Рис. 8.1.9. Решение уравнения с использованием Given

Содержание раздела



---







---