Решение нелинейных систем уравнений

MathCAD дает возможность находить решение системы уравнений численными методами, при этом максимальное число уравнений в MathCAD2001i доведено до 200.

Для решения системы уравнений необходимо выполнить следующие этапы.

Задание начального приближения для всех неизвестных, входящих в систему уравнений. При небольшом числе неизвестных этот этап можно выполнить графически, как показано в примере 8.2.2.

Пример 8.2.2. Дана система уравнений:

                                                           (8.2.7)

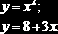
Определить начальные приближения для решений этой системы. Фрагмент документа MathCAD, приведенный на рис. 8.2.2, содержит построение графиков двух функций, входящих в систему (8.2.7), координаты точек пересечения этих графиков могут быть взяты в качестве начальных приближений.

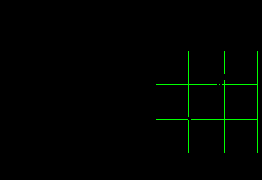
Рис. 8.2.2. Определение начальных приближений

Видно, что система имеет два решения: для первого решения в качестве начального приближения может быть принята точка (-2, 2), а для второго решения – точка (5, 20). ¨

Вычисление решения системы уравнений с заданной точностью (т.е. уточнение начального приближения). Для этого используется уже известный вычислительный блок Given, имеющий структуру (8.1.8). В этом блоке решаемые уравнения задаются в виде равенств, в которых используется «жирный» знак равно, вводимый с палитры Логический. Ограничения содержат равенства или неравенства, которым должно удовлетворять искомое решение.

Функция Find вычисляет решение системы уравнений с заданной точностью, и вызов этой функции имеет вид Find(x), где x – список переменных, по которым ищется решение. Начальные значения этим переменным задаются в блоке < Начальные условия >. Число аргументов функции должно быть равно числу неизвестных.

Следующие выражения недопустимы внутри блока решения:

• ограничения со знаком ¹;
• дискретная переменная или выражения, содержащие дискретную переменную в любой форме;




• блоки решения уравнений не могут быть вложены друг в друга, каждый блок может иметь только одно ключевое слово Given и имя функции Find (или Minerr).

Заметим, что, используя функцию Find, можно определить другую функцию пользователя. Например,
f(a, b, c, …):= Find(x, y, z, …).
Эта конструкция удобна для многократного решения системы уравнений для различных значений некоторых параметров a, b, c,…,
непосредственно входящих в систему уравнений.
Сообщение об ошибке

 (решение не найдено) при вычислении решения уравнений появляется, когда:

• поставленная задача может не иметь решения;


• для уравнения, которое не имеет вещественных решений, в качестве начального приближения взято вещественное число и наоборот;


• в процессе поиска решения последовательность приближений попала в точку локального минимума функционала невязки. Для поиска искомого решения нужно задать другие начальные приближения;


• возможно, поставленная задача не может быть решена с заданной точностью. Попробуйте увеличить значение TOL. Для этого необходимо обратиться к пункту меню Математика команда Опции в появившемся диалоговом окне в закладке Встроенные переменные изменить значение системной переменной TOL (по умолчанию она равна 0.001).

Если в процессе вычисления решения не может быть получено дальнейшее уточнение текущего приближения к решению, то функция Minner возвращает это приближение. Функция Find
в этом случае возвращает сообщение об ошибке.
Пример 8.2.3. Используя блок Given, вычислить все решения системы (8.2.7) примера 8.2.2. Выполнить проверку найденных решений. Фрагмент документа приведен на рис. 8.2.3. ¨



Рис. 8.2.3. Решение системы уравнений примера 8.2.2
Задание 8.2.1. Используя блок Given, вычислить все решения следующих систем уравнений:
А

 Б


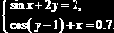
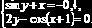
В

 Г


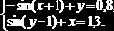
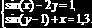
Проверить найденные решения. ?
Пример 8.2.4. Используя функцию

, вычислите решение системы уравнений



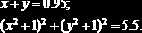
Фрагмент документа MathCAD показан на рис. 8.2.4. ¨



Рис. 8.2.4. Вычисление решения системы примера 8.2.4

Содержание раздела



---







---