Программирование и решение задач в пакете MathCAD
       

Решение оптимизационных задач с ограничениями


Используются те же функции Maximize, Minimize, но они входят уже в блок решения Given (см. (8.1.8)) и перед ними размещаются ограничения в виде равенств или неравенств, определяющие допустимую область значений параметров оптимизации.

Пример 9.2.1. Дан функционал:

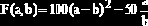
Решение оптимизационных задач с ограничениями
Решение оптимизационных задач с ограничениями
                                                      (9.2.1)

и ограничения в виде

Решение оптимизационных задач с ограничениями
                                                     (9.2.2)

Определить значения a, b, доставляющие максимальное значение функционала (9.2.1) и удовлетворяющие неравенствам (9.2.2).

Документ MathCAD, решающий эту задачу, показан на рис. 9.2.1. Точка «старта» алгоритма берется из допустимой области, определяемой ограничениями (9.2.2).

Решение оптимизационных задач с ограничениями

Рис. 9.2.1. Условная максимизация функционала (9.2.1)

 

Замечание 9.2.1. В оптимизационных задачах с ограничениями решение целесообразно определять из необходимых условий экстремума. Эти условия порождают систему уравнений (чаще всего нелинейных), которые располагаются в блоке Given, вместе с ограничениями, определяющими допустимую область. Само решение ищется с помощью функций Find, Minerr (подробно рассмотренных в п. 8.2.2).

Пример 9.2.2.

В качестве тестового функционала при поиске точки минимума часто используется функционал Розенброка:

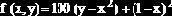
Решение оптимизационных задач с ограничениями
.                                     (9.2.3)

«Поверхность» этого функционала напоминает глубокий овраг, что сильно осложняет работу многих алгоритмов минимизации. Требуется вычислить точку минимума функционала при ограничениях:

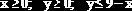
Решение оптимизационных задач с ограничениями
.                                                (9.2.4)

Документ MathCAD решения этой задачи показан на рис. 9.2.2.

Решение оптимизационных задач с ограничениями

Рис. 9.2.2. Минимизация функции Розенброка

 

Пример 9.2.3 (задача линейного программирования). Цех малого предприятия должен изготовить 100 изделий трех типов

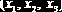
Решение оптимизационных задач с ограничениями
 и не менее 20 штук изделий каждого типа. На изделия уходит 4, 3.4 и 2 кг металла соответственно, при его общем запасе 340 кг, а также расходуются по 4.75, 11 и 2 кг пластмассы, при ее общем запасе 400 кг. Прибыль, полученная от каждого изделия равна 4, 3 и 2 р. Определить сколько изделий каждого типа необходимо выпустить для получения максимальной прибыли в рамках установленных запасов металла и пластмассы.


Документ MathCad, решающий эту задачу приведен на рис. 9.2.3.
Решение оптимизационных задач с ограничениями

Рис. 9.2.3. Решение задачи линейного программирования
Пример 9.2.4 (задача нелинейного программирования). Пусть вектор v состоит из трех проекций и дан функционал:
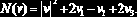
Решение оптимизационных задач с ограничениями

Вычислить точку минимума этого функционала при ограничениях:
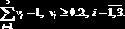
Решение оптимизационных задач с ограничениями

Документ MathCAD, решающий эту задачу, показан на рис. 9.2.4.
Решение оптимизационных задач с ограничениями

Рис. 9.2.4. Решение задачи нелинейного программирования
 
Задание 9.2.1 (задача линейного программирования). Дан функционал:
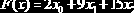
Решение оптимизационных задач с ограничениями
.
Определить точку максимума этого функционала при ограничениях:
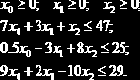
Решение оптимизационных задач с ограничениями

Вычислить значения функционала в этой точке.
Ответ: максимум функционала достигается в точке (0, 13, 8). ?
Задание 9.2.2 (задача квадратичного программирования). Дан функционал:
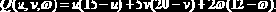
Решение оптимизационных задач с ограничениями

Определить точку максимума этого функционала при ограничениях:
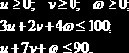
Решение оптимизационных задач с ограничениями

Ответ: максимум функционала достигается в точке (7.5, 10, 6).?

Содержание раздела



Главная сайта